Views: 0 Author: Site Editor Publish Time: 2025-12-30 Origin: Site








Collimation refers to the degree to which a laser beam remains parallel as it propagates over distance. An ideal collimated beam has perfectly parallel edges and never diverges, with a divergence angle of exactly 0. However, this is impossible in reality and only exists in some science fiction movies where laser beams extend infinitely with a constant diameter. In reality, laser beams inevitably diverge, and when the distance to the laser is sufficiently large, its intensity may even follow an inverse square law.

For coherent monochromatic light sources like lasers, the degree of divergence is mainly affected by the beam diameter (outgoing or beam waist) and wavelength. Specifically, the wider the beam, the smaller the divergence; the shorter the wavelength, the smaller the divergence. Short-sized lasers typically produce beams with stronger divergence, mainly because the beam diameter of these lasers is usually smaller, rather than directly caused by their size. This characteristic stems from the diffraction limit of wave propagation and cannot be overcome by optical elements; a beam that is both narrow and has low divergence simply does not exist.

(Refer to the diagram “Diffusion Angle, Beam Waist, Rayleigh Length”. Note that the diffusion angle in the diagram is greatly exaggerated, and the beam waist of most common lasers is actually located inside the resonant cavity or on a certain mirror.)
The formula for the total divergence angle (in radians) of a plane wave source is:

To calculate the half-angle divergence angle (as indicated in some laser specifications), simply divide the result by 2. This formula and the inverse square law of light intensity only apply to scenarios where the distance from the laser exceeds the Rayleigh length (much greater than the beam waist), and require ideal conditions to be met—given the beam (beam waist) diameter, the far-field divergence angle cannot be further reduced without re-collimation.
It should be noted that the position of the effective point source usually does not coincide with the laser's exit aperture; similarly, the beam diameter does not necessarily refer to the spot size when the beam exits the resonant cavity, but may be the beam waist diameter (which can be located inside or outside the resonant cavity). The optical components of the resonant cavity (such as the curvature of the mirrors, the external curvature of the output coupling mirror, etc.) will affect the beam waist.

The basic formula for the diffraction-limited spot size of an ideal Gaussian beam is:
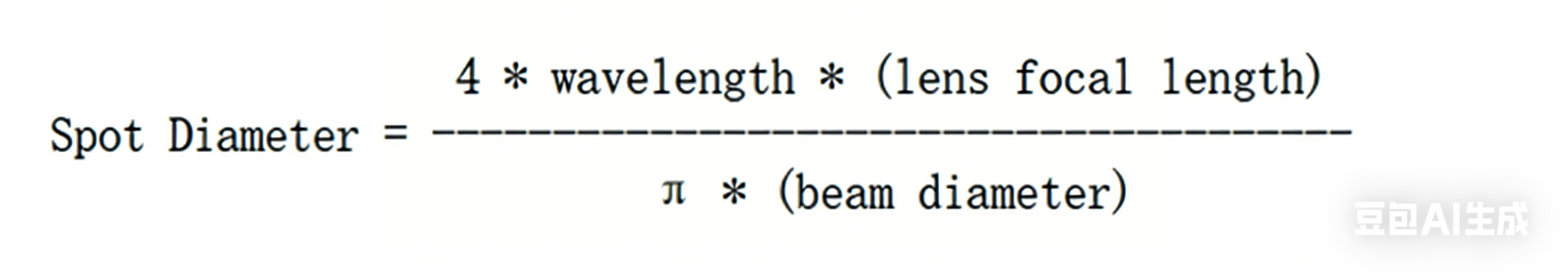
Since "lens focal length / beam diameter" essentially reflects the converging speed of the beam, and is also the "f-number" of the optical system, the above formula can be equivalently expressed as:

To calculate the required lens focal length based on the target spot size, the formula is as follows:

If the M² value of the beam is not equal to 1 (non-circular TEM₀₀ fundamental mode Gaussian beam), the final spot size will increase; if the beam diameter is rigidly limited by the aperture, 4/π in the formula needs to be replaced with 2.44, and the calculated result is the spot diameter corresponding to the first dark fringe.
An ideal helium-neon laser has an aperture of 0.5 mm, a wavelength of 632.8 nm, and a divergence angle of approximately 1.6 milliradians. Using a lens with a focal length of 25 mm, the minimum spot size is approximately 40.28 micrometers. If the beam is first expanded to 10 mm and collimated, and then focused using the same lens, the spot size can be reduced to slightly larger than 4 micrometers.
Some laser specifications will include a "millimeter-mRad (mm-mRad)" parameter. This parameter represents the product of the beam size (in millimeters) at the incident plane, near-field plane, or beam waist (where the beam is at its smallest size) and the far-field angular divergence (in milliradians). It's important to note that different manufacturers may define "beam size" differently, including full width, half-width, half-height full width, 1/e width, 1/e² width, first dark fringe width, standard deviation, width containing 86% of the energy, etc.

BU-LASER provides Semiconductor diode lasers with violet, cyan, blue, green, red and infrared color (375nm- 1064nm, 1mW-500W output power, different beam mode, and dimensions) to better meet customers’ needs of different applications. We also offer professional OEM &ODM service! To know more, please get in touch with us at song@bu-laser.com.